Inverting Amplifier

Introduction

An amplifier is an analogue circuit. This page is about a voltage amplifier based on an Op-Amp. The output voltage (V_out) of the circuit depends on the input voltage (V_in) and the Gain (A_v) of the circuit.

It is a good idea to read the amplifier basics page first.

For all the circuits shown below, the amplifier is assumed to have a positive and a negative power supply, usually ±15 V, so that the output voltage can be both positive and negative.

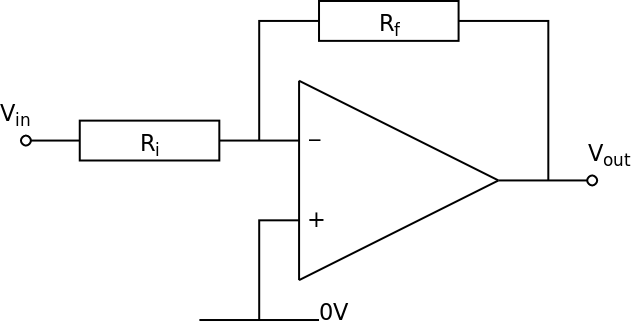
Basic Inverting Amplifier Circuit

Inverting Amplifier Circuit

The Op-Amp needs to have ± power supplies (assumed to be ±15 V)

The non-inverting input is connected to 0 V

The circuit uses a feedback resistor (R_f) and an input resistor (R_i)

Voltage gain (A_v) is determined by R_f and R_i

The voltage gain is given by:

A_v = −R_f / R_i

Note: R_i and R_f should both be > 1 kΩ and < 10 MΩ

Function of the Inverting Amplifier

The output voltage is directly proportional to the input voltage (as long as the output is not saturated) such that:

V_out = A_v × V_in

Note: If A_v < 1, V_out < V_in and the input voltage has been attenuated rather than amplified

If the input voltage is positive, the output voltage is negative

If the input voltage is negative, the output voltage is positive

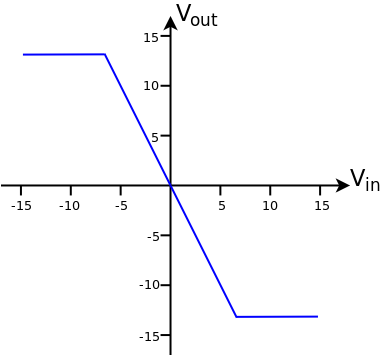The graph shows the transfer characteristics (Input Voltage and Output Voltage) for an Inverting amplifier with a voltage Gain of −2

When V_in = +5 V then V_out = −10 V

when V_in = −5 V then V_out = +10 V

The Output Voltage is limited to ±13 V by the power supply of the amplifier. Therefore, when V_in > +6.5 V then V_out saturates at −13 V and when V_in < −6.5 V then V_out saturates at +13 V. The saturated output is shown by the horizontal lines on the graph.

AC gain The graph shows the relationship between the Input Voltage and Output Voltage of an Inverting amplifier with a voltage Gain of −2 when the input is an A.C. voltage

At all times V_out = −2 × V_in

Example Circuits

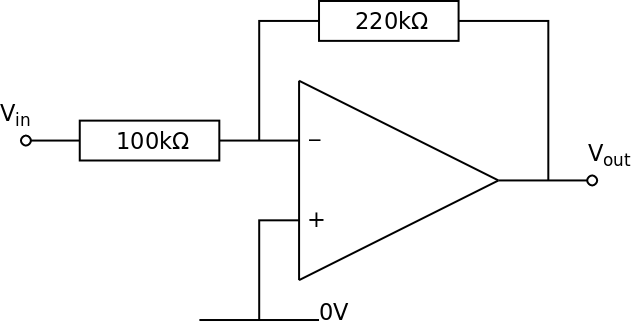Example 1 The voltage gain is:

A_v = − 220 ×10³ / 100 ×10³ = −2.2

If V_in = +1.0 V then V_out = −2.2 V

The Input Voltage has been amplified (made bigger)

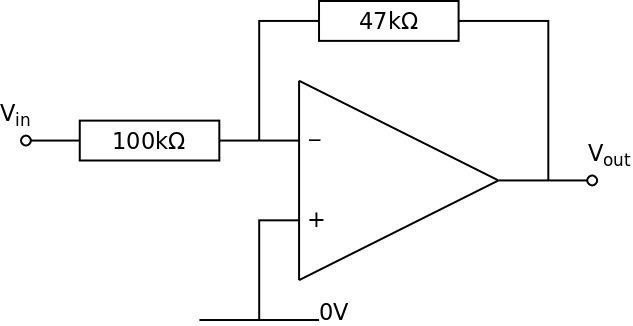Example 2 The voltage gain is:

A_v = − 47 ×10³ / 100 ×10³ = −0.47

If V_in = +1.0 V then V_out = −0.47 V

The Input Voltage has been attenuated (made smaller)

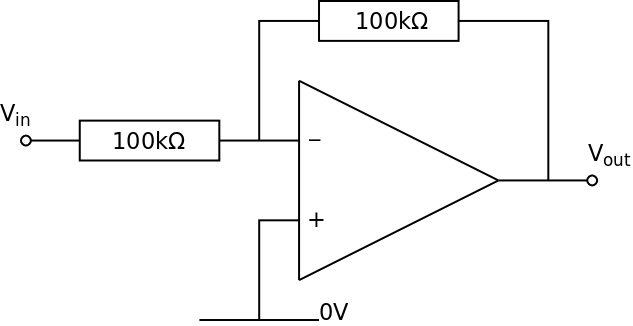Example 3 The voltage gain is:

A_v = − 100 ×10³ / 100 ×10³ = −1.0

If V_in = +1.0 V then V_out = −1.0 V

This is a unit gain amplifier. The Output Voltage has the same amplitude as the Input Voltage. This amplifier is a buffer as the input takes almost no current from the voltage source but provides a reasonable current to the subsequent circuits

Example 4 The voltage gain is:

A_v = − 100 / 100 = −1.0

This is a poor circuit as the resistor values are too small. The amplifier will draw too much current from the source. Resistor values should always be greater than 1 kΩ

Gain and Bandwidth

The two main parameters of the Inverting Amplifier are the gain and the bandwidth. Increasing the gain reduces the bandwidth and vice versa.

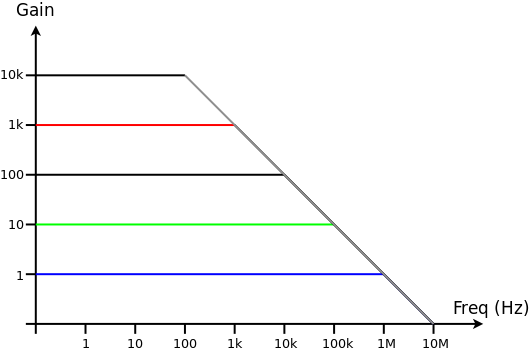
Gain vs Bandwidth For an inverting amplifier based on a standard Op-Amp the relationship between gain and bandwidth is approximately:

gain × bandwidth = 10⁶

The graph shows that as gain increases, bandwidth decreases. Note that both scales are logarithmic. The Gain axes shows the magnitude of the gain and the negative sign is ignored

When the gain is ×1 (blue line) the amplifier works effectively up to frequencies of 1 MHz

If the gain is increased to ×10 (green line) the amplifier only works effectively up to about 100 kHz. This is still suitable for audio

At a gain of ×1000 (red line) the amplifier only works effectively up to a frequency of 1 KHz before the gains starts to reduce and the Output voltage starts to decrease

If the gain is −100, the bandwidth is 10 kHz

If a bandwidth of 40 kHz is required, the maximum gain is −25

Better Inverting Amplifier Circuit

When used in reality, amplifiers are often decoupled which means that the input and output are connected through capacitors to stop any spurious D.C. signals compromising the performance of the amplifier. Depending on what circuit or transducer the amplifier is attached to, a resistor may also be needed on the output down to 0 V.

with capacitors The capacitor on the input is usually a non-electrolytic type, nominally 1 µF or less. The capacitor on the output is ideally a non-electrolytic type but sometimes larger value electrolytic capacitors need to be used if the amplifier is providing significant current to the next stage.

The addition of capacitors to the input and output can reduce the bandwidth of the amplifier.

How the Inverting Amplifier works (Advanced)

When considering amplifiers made from Op-Amps there are two basic assumptions:

The open loop gain (A₀) of the Op-Amp is very large
No current flows in to the inverting and non-inverting inputs

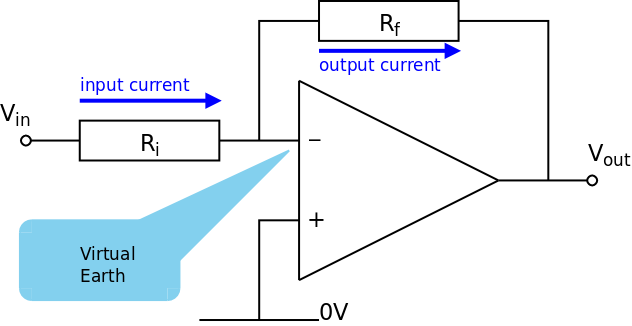
virtual earth

Negative Feedback

Recall that V_out = A₀ × (V₊ − V₋) where A₀ = 10⁶ and so a difference between V₊ and V₋ of more than a few µV will result in a large (saturated) output voltage
The feedback resistor ensures that voltage at the inverting input is very similar (within a few microvolts) to the voltage at the non-inverting input
As the non-inverting input is connected to ground (0 V) then the inverting input must also be very close to 0 V and is called a virtual earth
R_i and R_f form a potential divider with V_in at one end, V_out at the other end and the inverting input at approximately 0 V in the middle
The feedback works because if V_in is positive and rises, the voltage at the inverting input rises as a consequence. This increases the difference between the inverting and non-inverting inputs and causes V_out to change. As the inverting input is bigger than the non-inverting input in this case then V_out becomes more negative. As V_out becomes more negative the voltage at the inverting input falls again until it is approximately 0 V once more. Therefore a change in the input voltage causes an opposing change in the output voltage to keep the inverting input at (or very close to) zero

Gain Equation

Assume V_in is positive (as shown in the diagram above)
The current in the input resistor is given by I = V_in / R_i because the virtual earth means that the V_in is the potential difference across the resistor
As no current flows in to the inverting input, the current in the input resistor also flows through the feedback resistor
To make the current flow from the virtual earth in the direction shown V_out must be negative
Therefore I = −V_out / R_f
Equating the currents leads to the gain equation
Recall, gain is defined as: Gain = V_out / V_in

We have

I = V_in / R_i = −V_out / R_f

and therefore

Gain = V_out / V_in = −R_f / R_i