It is important to be able to analyse a logic circuit that contains several logic gates and has two or three inputs.
To analyse the behaviour of a logic circuit a truth table can be used. As well as the inputs and the output, extra columns are added for the intermediate points in the logic circuit.
Note: Logic circuits can also be analysed using Boolean Algebra or Karnaugh Maps but this page only considers basic truth tables.
 A and B are the inputs. The aim is to find the output Q for all possible combinations of A and B.
A and B are the inputs. The aim is to find the output Q for all possible combinations of A and B.
Step 1: Fill in columns A and B with all possible combinations of 0 and 1 - in this case there are only four possible combinations.
Step 2: Add intermediate columns X and Y for the outputs of the first two logic gates.
Step 3: Fill in column X where X is the output of an AND gate and so X=1 when A=1 AND B=1, otherwise X=0.
Step 4: Fill in column Y where Y is the output of an OR gate and so Y=1 when A=1 OR B=1, otherwise Y=0.
Step 5: Fill in the column for the output Q where Q is the output of an OR gate that has X and Y as the inputs. Therefore Q=1 when X=1 OR Y=1, otherwise Q=0.
Note: This whole circuit can be simplified to a single OR gate with A and B as the inputs.
 A and B are the inputs. The aim is to find the output Q for all possible combinations of A and B.
A and B are the inputs. The aim is to find the output Q for all possible combinations of A and B.
Step 1: Fill in columns A and B with all possible combinations of 0 and 1 - there are only four possible combinations.
Step 2: Add intermediate columns X as the output of the AND gate and Y as the output of the NOT gate.
Step 3: Fill in column X where X is the output of an AND gate and so X=1 when A=1 AND B=1, otherwise X=0.
Step 4: Fill in column Y where Y is the output of the NOT gate so when B=0, Y=1 and when B=1, Y=0.
Step 5: Fill in the column for the output Q where Q is the output of the OR gate that has X and Y as the inputs. Therefore Q=1 when X=1 OR Y=1, otherwise Q=0.
 A, B and C are the inputs. The aim is to find the output Q for all possible combinations of A, B and C.
A, B and C are the inputs. The aim is to find the output Q for all possible combinations of A, B and C.
Step 1: Fill in columns A, B and C with all possible combinations of 0 and 1 - there are eight possible combinations.
Step 2: Add intermediate columns X, Y and Z as the outputs the two OR gates and the NOT gate.
Step 3: Fill in column X where X is the output of an OR gate with A and B as the inputs so X=1 when A=1 OR B=1, otherwise X=0.
Step 4: Fill in column Y where Y is the output of the NOT gate so when B=0, Y=1 and when B=1, Y=0.
Step 5: Fill in column Z where Z is the output of the OR gate with Y and C as the inputs so Z=1 when C=1 OR Y=1, otherwise Z=0.
Step 6: Fill in the column for the output Q where Q is the output of the AND gate that has X and Z as the inputs. Therefore Q=1 when X=1 AND Z=1, otherwise Q=0.
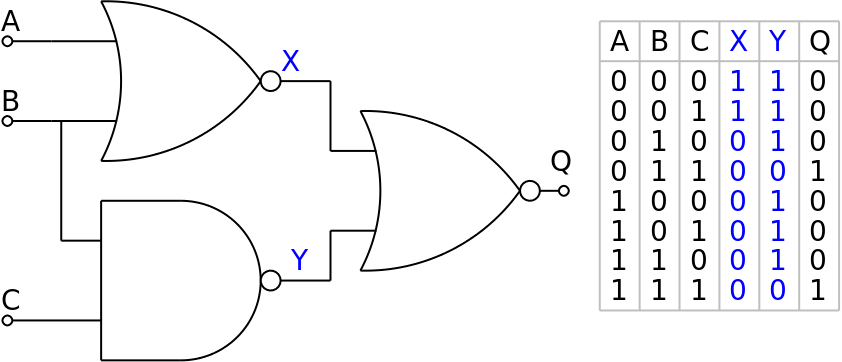 A, B and C are the inputs. The aim is to find the output Q for all possible combinations of A, B and C.
A, B and C are the inputs. The aim is to find the output Q for all possible combinations of A, B and C.
Step 1: Fill in columns A, B and C with all possible combinations of 0 and 1 - there are eight possible combinations.
Step 2: Add intermediate columns X as the output of the first NOR gate and Y as the output of the NAND gate.
Step 3: Fill in column X where X is the output of a NOR gate and so X=0 when A=1 OR B=1, otherwise X=1.
Step 4: Fill in column Y where Y is the output of the NAND gate so Y=0 when B=1 AND C=1, otherwise Y=1.
Step 5: Fill in the column for the output Q where Q is the output of the NOR gate that has X and Y as the inputs. Therefore Q=0 when X=1 OR Y=1, otherwise Q=1.
Note: This whole circuit can be simplified to a single AND gate with B and C as the inputs, the value of input A is irrelevant.
© Paul Nicholls
January 2018

Electronics Resources by Paul Nicholls is licensed under a Creative Commons Attribution 4.0 International License.