Potential dividers are a very common part of even the most complex circuits and it is therefore very important to understand what they do and how to do the associated calculations. Luckily potential dividers are one of the most simple circuits you can build and so understanding them shouldn't be too hard.
 A potential divider is a pair of resistors connected in series and connected to a power supply or other source of EMF (voltage). The potential difference across ONE of the resistors is a fraction of the applied EMF. The total potential difference across the resistors is divided between the two resistors, each having its own potential difference - hence potential divider.
A potential divider is a pair of resistors connected in series and connected to a power supply or other source of EMF (voltage). The potential difference across ONE of the resistors is a fraction of the applied EMF. The total potential difference across the resistors is divided between the two resistors, each having its own potential difference - hence potential divider.
In essence, a potential divider is a circuit with an input and an output. You apply a voltage to the input (Vin) and get a smaller voltage at the output (Vout). The output voltage is a fraction of the input voltage.
The output voltage depends on (a) the input voltage and (b) the ratio of the two resistors.
Note: The output voltage does not depend on the actual value of the individual resistors, it depends on the ratio of the pair of resistors - they work together and the output of the potential divider depends on their relative values.
 The output voltage from a potential divider (Vout) is given by the potential divider equation:
The output voltage from a potential divider (Vout) is given by the potential divider equation:
It is important to be able to use this equation.
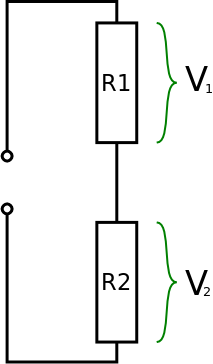 The potential divider equation is very useful for calculating Vout but it is less obvious when trying to calculate R1 or R2. It is usually much easier to use the ratios of the voltages to work out what resistor values to use. The ratio of the voltages is equal to the ratio of the resistances:
The potential divider equation is very useful for calculating Vout but it is less obvious when trying to calculate R1 or R2. It is usually much easier to use the ratios of the voltages to work out what resistor values to use. The ratio of the voltages is equal to the ratio of the resistances:
or
or
Knowing Vin and Vout means you know V1 and V2 (V2 is Vout of course). Once you know V1 and V2 you can choose R1 and R2 accordingly
 The potential divider equation relies on the fact that the current in R1 is the same as the current in R2 and no current flows in the load (the load has an infinite resistance). If this is NOT the case, the potential divider equation will not give a correct value for Vout and neither will the method of using ratios.
The potential divider equation relies on the fact that the current in R1 is the same as the current in R2 and no current flows in the load (the load has an infinite resistance). If this is NOT the case, the potential divider equation will not give a correct value for Vout and neither will the method of using ratios.
When calculating values of Vout, R1 or R2 it is always assumed that no current flows from the output of the potential divider
In reality, this is not possible to achieve. Any load such as a voltmeter or subsystem connected to the output of the potential divider will always take some current. However, the theory is very nearly correct when the current flowing from the potential divider to the load is much less than the current through R1 and R2. In practice, the values of R1 and R2 should be several orders of magnitude smaller than the resistance of the load.
For example, if a voltmeter has a resistance of 1 MΩ then a potential divider made from a pair of 10 kΩ resistors will work as expected but a potential divider made from a pair of 500 kΩ resistors will give a value of Vout smaller than expected.
Note: The finite resistance of the load is effectively in parallel with R2 which reduces the overall combined resistance of R2 and therefore reduces Vout.
Link to an Interactive White Board Presentation showing the derivation of the Potential Divider Equation.
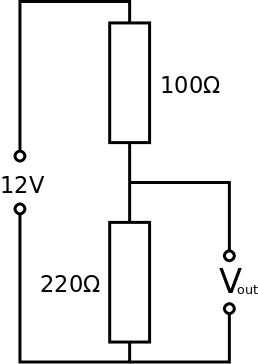 Example 1: Given the two resistor values and the supply voltage, find the output voltage.
Example 1: Given the two resistor values and the supply voltage, find the output voltage.
The values given are non trivial so the best approach is to use the equation for Vout
Therefore:
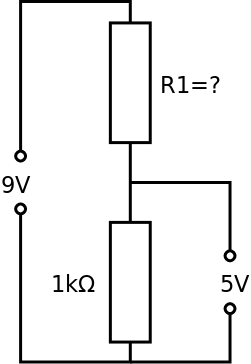 Example 2: Given Vout = 5 V, Vin = 9 V and R2 = 1 kΩ calculate R1.
Example 2: Given Vout = 5 V, Vin = 9 V and R2 = 1 kΩ calculate R1.
The best approach when trying to find a resistor value is to use the method of ratios.
The voltage across R2 is 5 V and therefore the voltage across R1 is 4 V
Therefore:
 Example 3: Given Vout = 2 V, Vin = 6 V and R1 = 12 kΩ calculate R2.
Example 3: Given Vout = 2 V, Vin = 6 V and R1 = 12 kΩ calculate R2.
Again, the best approach when trying to find a resistor value is to use the method of ratios.
The voltage across R2 is 2 V and therefore the voltage across R1 is 4 V
Therefore:
Link to an Interactive White Board Presentation showing examples of Potential Divider calculations.
Where one of the resistors in a potential divider is variable - an LDR or Thermistor for example - it is very important to know how Vout changes when either R1 or R2 changes (and Vin remains fixed).
 Case 1: R1 increases
Case 1: R1 increases
R1 increases and takes a larger share of the input voltage
Therefore, the remaining voltage, Vout goes down
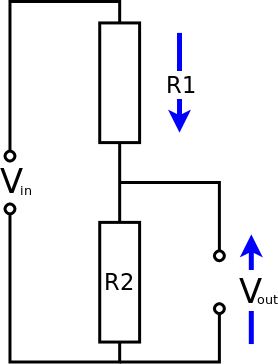 Case 2: R1 decreases
Case 2: R1 decreases
R1 decreases and takes a smaller share of the input voltage
Therefore, Vout goes up
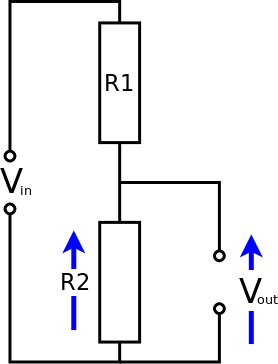 Case 3: R2 increases
Case 3: R2 increases
R2 increases and takes a larger share of the input voltage
Therefore, Vout goes up
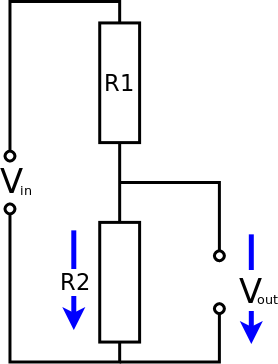 Case 4: R2 decreases
Case 4: R2 decreases
R2 decreases and takes a smaller share of the input voltage
Therefore, Vout goes down
Consider (and learn and understand) each of the following examples:
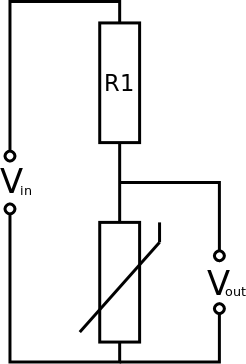 Thermistor as R2:
Thermistor as R2:
As the temperature increases the resistance of the thermistor decreases. As the resistance decreases, Vout decreases.
Therefore, Vout goes down as the temperature increases
As the temperature decreases the resistance of the thermistor increases. As the resistance increases, Vout increases.
Therefore, Vout goes up as the temperature decreases
A similar situation occurs if an LDR is used in place of R2. If the light level increases, Vout goes down and vice versa
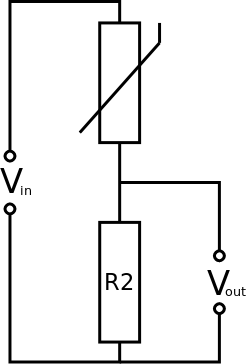 Thermistor as R1
Thermistor as R1
As the temperature increases the resistance of the thermistor decreases. As the resistance decreases, Vout increases.
Therefore, Vout goes up as the temperature increases
As the temperature decreases the resistance of the thermistor increases. As the resistance increases, Vout decreases.
Therefore, Vout goes down as the temperature decreases
A similar situation occurs if an LDR is used in place of R1. If the light level increases, Vout goes up and vice versa
© Paul Nicholls
January 2016

Electronics Resources by Paul Nicholls is licensed under a Creative Commons Attribution 4.0 International License.