Resistors are physically quite small most of the time and so it is inconvenient to simply write the value and tolerance on the resistor. A clear but compact code is needed.
On circuit diagrams it is important not to miss the decimal place and use a 47 kΩ resistor instead of a 4.7 kΩ so clarity is required.
The Resistor Colour Code uses coloured bands to make it easy to identify resistor values and tolerances and the Resistor Printed Code (BS1852) gives a standard for printed markings on resistors and on circuit diagrams.
Surface mounted devices and some other resistors use a numerical version of the colour code using three digits to represent any value of resistor.
The resistor colour code uses 10 different colours to represent the value of the resistor. A different set of colours is used to represent other information such as the tolerance or thermal stability. It is worth knowing what the colours represent as it makes life easier when building circuits.
For the bands representing the value, the colour code is:
Black = 0
Brown = 1
Red = 2
Orange = 3
Yellow = 4
Green = 5
Blue = 6
Violet = 7
Grey = 8
White = 9
For the tolerance band, the colour code is:
Brown = ± 1%
Red = ± 2%
Gold = ± 5%
Silver = ± 10%
Blank = ± 20%
In many cases, such as in schools, the resistors used are all ± 5% or worse. Therefore there is no point in giving the value to a high level of precision using many significant figures. Resistor values are usually given to 2 significant figures. The value is given as the 2 most significant digits and then the relevant number of zeros. For example, a resistance of 127.5 Ω is simple given as 130 Ω or 13 followed by one zero.



The BS1852 Printed Resistor Code uses letters and numbers to signify the value of the resistor.
Tolerance is indicated by adding a letter at the end:
 A 220 Ω resistor with a tolerance of ± 5% is written as 220 R J (220 × 1 = 220 Ω)
A 220 Ω resistor with a tolerance of ± 5% is written as 220 R J (220 × 1 = 220 Ω)
 A 4700 Ω resistor with a tolerance of ± 5% is written as 4 K 7 J (4.7 × 1000 = 4700 Ω)
A 4700 Ω resistor with a tolerance of ± 5% is written as 4 K 7 J (4.7 × 1000 = 4700 Ω)
 A 10,000 Ω resistor with a tolerance of ± 5% is written as 10 K J (10 × 1000 = 10000 Ω)
A 10,000 Ω resistor with a tolerance of ± 5% is written as 10 K J (10 × 1000 = 10000 Ω)
Small value resistors - between 10 Ω and 100 Ω are often identified wrongly. The third band in this case is always black which means that there are NO zeros following the value. It is all too easy to read the third band as zero and assume that the zero follows the value ... it does not! Black means there are zero zeros after the value!



Low value resistors - those less than 10 Ω - use the THIRD coloured band to reduce the value of the resistor by dividing by either 10 or 100. The first two coloured bands give the value of the resistor and the third coloured band divides the value to make it smaller.
Gold ÷ 10
Silver ÷ 100
For example, a 4.7 Ω ± 5% resistor is 47 Ω ÷ 10 and would therefore be Yellow, Violet, Gold, Gold
Similarly, a 0.56 Ω ± 1% resistor is 56 Ω ÷ 100 and would therefore be Green, Blue, Silver, Brown

A resistor with a value of 0 Ω is useful as a wire link. The reason why a zero ohm resistor is better than a simple piece of wire is that the same machines that fit resistors into circuit boards on production lines can also be used to fit the "wire links" to the circuit boards. A zero ohm resistor has a single black band.
For resistors with a tolerance of better than ± 5%, more than two significant figures are needed to represent the value.
High precision resistors have THREE bands for the value and then one band for the number of zeros - four bands in total to represent the value. The colour code otherwise works in exactly the same way. Note: 5th band gives tolerance where Brown = ± 1%.

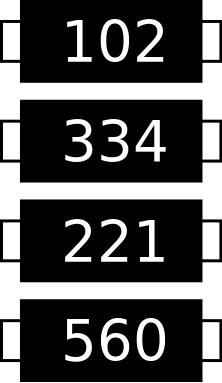 A slightly different approach is used for surface mounted resistors, some other resistors and low value capacitors. The format of the colour code is retained but the colours are replaced by printed numbers. The 2 significant figures and then a 3rd digit representing the multiplying factor (number of zeros) are simply printed on the device / resistor and there is no tolerance indicated. The first two numbers represent the value and the 3rd number represents the number of zeros. Therefore, if the 3rd digit is 4, multiply by 10,000 (4 zeros) but if the 3rd digit is 1 just multiply by 10. If the 3rd digit is 0, multiply by 1 - there are no extra zeros.
A slightly different approach is used for surface mounted resistors, some other resistors and low value capacitors. The format of the colour code is retained but the colours are replaced by printed numbers. The 2 significant figures and then a 3rd digit representing the multiplying factor (number of zeros) are simply printed on the device / resistor and there is no tolerance indicated. The first two numbers represent the value and the 3rd number represents the number of zeros. Therefore, if the 3rd digit is 4, multiply by 10,000 (4 zeros) but if the 3rd digit is 1 just multiply by 10. If the 3rd digit is 0, multiply by 1 - there are no extra zeros.
102 = 1 0 × 100 = 1000 Ω (10 followed by two zeros is 1000 Ω)
334 = 3 3 × 10,000 = 330 kΩ (33 followed by four zeros is 330,000 Ω)
221 = 2 2 × 10 = 220 Ω (22 followed by one zero is 220 Ω)
560 = 5 6 × 1 = 56 Ω (56 followed by no (zero) zeros is 56 Ω)
 The pcb mounted potentiometers shown are all different values. The value is shown by the three digit code and there is no tolerance. From left to right the values are:
The pcb mounted potentiometers shown are all different values. The value is shown by the three digit code and there is no tolerance. From left to right the values are:
502 = 5 0 × 100 = 5 kΩ (50 followed by two zeros = 5000 Ω)
503 = 5 0 × 1000 = 50 kΩ (50 followed by three zeros = 50,000 Ω)
103 = 1 0 × 1000 = 10 kΩ (10 followed by three zeros = 10,000 Ω)
104 = 1 0 × 10,000 = 100 kΩ (10 followed by four zeros = 100,000 Ω)
Resistors with a tolerance of ± 10% (Silver) form a series of 12 values, each approximately 20% bigger than the last. This series is called the E12 series.
The E12 series is:
10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68, 82
... and all the subsequent decades / powers of 10
Examples of E12 values include: 100Ω, 15kΩ, 220Ω, 330kΩ, 4.7Ω, 6.8MΩ, 10kΩ, 1kΩ
Resistors with a tolerance of ± 5% (Gold) form a series of 24 values, each approximately 10% bigger than the last. This series is called the E24 series.
The E24 series is:
10, 11, 12, 13, 15, 16, 18, 20, 22, 24, 27, 30, 33, 36, 39, 43, 47, 51, 56, 62, 68, 75, 82, 91
... and all the subsequent decades / powers of 10
Examples of E24 values include: 110Ω, 13kΩ, 200Ω, 360kΩ, 4.3Ω, 6.2MΩ, 11kΩ, 1k3Ω
© Paul Nicholls
January 2016

Electronics Resources by Paul Nicholls is licensed under a Creative Commons Attribution 4.0 International License.