When two (or more) resistors are connected in series or in parallel, they are equivalent to just a single resistor but of a different value.
 Connecting two 100 Ω resistors in series in a circuit has the same effect as using a single 200 Ω resistor. The two 100 Ω resistors can be replaced by a single 200 Ω resistor or a single 200 Ω resistor can be replaced by two 100 Ω resistors in series - they are completely equivalent.
Connecting two 100 Ω resistors in series in a circuit has the same effect as using a single 200 Ω resistor. The two 100 Ω resistors can be replaced by a single 200 Ω resistor or a single 200 Ω resistor can be replaced by two 100 Ω resistors in series - they are completely equivalent.
The general principle is: For resistors in series, the total resistance is greater than any of the individual resistances. For two resistors R1 and R2 having an equivalent resistance Rt, Rt > R1 and Rt > R2.
Mathematically, the resistor combination rule for two resistors is very straight forward:
And for more than two resistors, the combination rule is simply:
The special case of two equal value resistors is worth remembering: For two resistors, each of value R, in series the total resistance is 2R.
Examples:
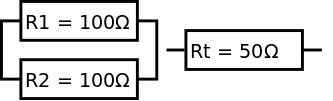 Connecting two 100 Ω resistors in parallel in a circuit has the same effect as using a single 50 Ω resistor. The two 100 Ω resistors in parallel can be replaced by a single 50 Ω resistor or a single 50 Ω resistor can be replaced by two 100 Ω resistors in parallel - once again they are completely equivalent.
Connecting two 100 Ω resistors in parallel in a circuit has the same effect as using a single 50 Ω resistor. The two 100 Ω resistors in parallel can be replaced by a single 50 Ω resistor or a single 50 Ω resistor can be replaced by two 100 Ω resistors in parallel - once again they are completely equivalent.
The general principle is: For resistors in parallel, the total resistance is smaller than any of the individual resistances. For two resistors R1 and R2 having an equivalent resistance Rt, Rt < R1 and Rt < R2.
Mathematically, the resistor combination rules for resistors in parallel are slightly more complex and must be used with care.
For two resistors in parallel:
or, alternatively:
For more than two resistors in parallel:
The special case of two equal value resistors is again worth remembering: For two resistors, each of value R, in parallel the total resistance is ½R.
Examples:
A good question is "why do you need to combine resistors? Why not just use the desired value in the first place?". The answer is because (a) you want a non-standard value or (b) you need more power handling capability.
Resistors come in standard values, the most common set of resistor values is the E24 series. In this series of resistors, the standard values are: 10, 11, 12, 13, 15, 16, 18, 20, 22, 24, 27, 30, 33, 36, 39, 43, 47, 51, 56, 62, 68, 75, 82, 91 and the corresponding powers of 10 for each of these values.
Getting the non-standard values:
If you need a value of 190 Ω it isn't available in the E24 series - the nearest values are either 180 Ω or 200 Ω. Therefore a 100 Ω and a 91 Ω resistor can be used in series to give a value of 191 Ω - which is close enough given a ± 5% uncertainty!
If you need a 310 Ω resistor, connect two 620 Ω resistors in parallel ... or a 200 Ω and a 110 Ω resistor in series ... there is always more than one way to make a resistor of the desired value.
To make a 26 kΩ resistor use a 10 kΩ resistor in series with a 16 kΩ resistor OR use a 24 kΩ in series with a 2 kΩ ... and so it goes on.
Note: Remember resistors have a tolerance so there is no validity in combining lots of resistors to get an "exact" value. Assuming our resistors have a 5% tolerance, there is no point in combining a 1 kΩ resistor and a 33 Ω resistor in series hoping to make a 1033 Ω resistor, the 5% tolerance on the 1 kΩ resistor is already + 50 Ω, an uncertainty bigger than the 33 Ω that was added! Think about what you are doing before you start adding loads of smaller and smaller resistors in series.
Increasing the power handling:
Resistors all have a maximum power rating. If you have a pile of resistors all rated at 1 W maximum power rating then, combining two or more of these in series or parallel will result in an equivalent resistor with a higher power rating - the power is shared between the resistors that have been combined.
Combining two such 10 Ω 1 W resistors in parallel will be equivalent to a 5 Ω resistor with a 2 W power rating. The situation is only slightly more complex if the resistors don't have the same value, for example, a 10 Ω resistor in series with a 22 Ω resistor produces a 32 Ω resistor with a power rating greater than 1 W.
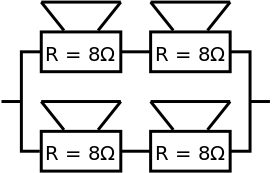 A special case worth mentioning is when dealing with loudspeakers (thinking of loudspeakers as essentially the same as resistors). Loudspeakers nominally have a resistance of 8 Ω and can handle a certain power. To ensure the audio system works most efficiently, loudspeakers must always have a resistance of 8 Ω. Therefore, to increase the power handling, we need to combine the loudspeakers in both series and parallel to produce an arrangement that still has a resistance of 8 Ω but a greater power handling. The diagram shows how this is accomplished. The two 8 Ω speakers in series add up to 16 Ω - the two 16 Ω pairs add up in parallel to make 8 Ω in total. A notable exception is in the case of P.A. system speakers that often have a resistance of only 4 Ω and speakers used in car audio systems where the speaker resistance can be even lower.
A special case worth mentioning is when dealing with loudspeakers (thinking of loudspeakers as essentially the same as resistors). Loudspeakers nominally have a resistance of 8 Ω and can handle a certain power. To ensure the audio system works most efficiently, loudspeakers must always have a resistance of 8 Ω. Therefore, to increase the power handling, we need to combine the loudspeakers in both series and parallel to produce an arrangement that still has a resistance of 8 Ω but a greater power handling. The diagram shows how this is accomplished. The two 8 Ω speakers in series add up to 16 Ω - the two 16 Ω pairs add up in parallel to make 8 Ω in total. A notable exception is in the case of P.A. system speakers that often have a resistance of only 4 Ω and speakers used in car audio systems where the speaker resistance can be even lower.
Example 1:

Two resistors in series are easy to add up but, in this example, it is important to make sure the units are correct: 4k7 Ω = 4700 Ω
Example 2:

As in the first example, ensure the units are correct.
and therefore
Example 3:

This example has to be considered in two parts as there are both parallel and series resistors. First R1 and R2 need to be added in parallel. Then, the series resistor R3 is added to give the total resistance of the three resistors.
Considering the parallel pair of R1 and R2 (and using the alternative form of the parallel resistor equation)
Adding R3 in series gives
Example 4:
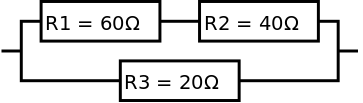
In this example there are also series and parallel resistors combined. In this case the series resistors R1 and R2 must be combined first. The result is then combined in parallel with R3.
Considering the series pair R1 and R2
Adding R3 in parallel gives
Example 5:

In this more complex example the resistors must once again be combined in pairs in the correct order. First R1 and R2 are added in parallel. Next the series resistor R3 is added to the previous result. Finally the total of R1, R2 and R3 is added in parallel to R4 ... simple!
Considering R1 and R2 in parallel
Adding R3 gives
Finally, adding R4 in parallel with the 40 Ω combination gives
There are two Interactive White Board resources and a Video available for download for this topic.
© Paul Nicholls
January 2016

Electronics Resources by Paul Nicholls is licensed under a Creative Commons Attribution 4.0 International License.