RC timing circuits are very important in electronics because they can be used to make time delay circuits and clock circuits. Clock circuits provide regular pulses that allow digital circuits to remain synchronized. Clock circuits are the heartbeat of our modern electronic world.
The topic heading "RC Timing Networks" can be a little hard to understand at first glance:
Read the capacitors page first
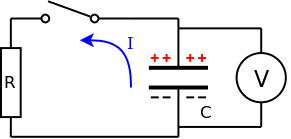
 The capacitor is initially uncharged and the voltmeter therefore reads zero
The capacitor is initially uncharged and the voltmeter therefore reads zero
When the switch is closed, current flows from the battery, through the resistor and charges the capacitor
Initially the capacitor is uncharged and the voltage across the capacitor is zero, therefore the voltage across the resistor is the battery voltage and the current is high - the capacitor charges quickly
After some time, the capacitor is partially charged. The voltage across the capacitor is not zero and the voltage across the resistor is less than the supply voltage, the current has been reduced and the capacitor charges more slowly
After a long time the capacitor is (almost) fully charged, the voltage across the capacitor is (almost) the battery voltage and the voltage across the resistor is (almost) zero. There is only a very small current (if any) and the capacitor charges very slowly towards being fully charged
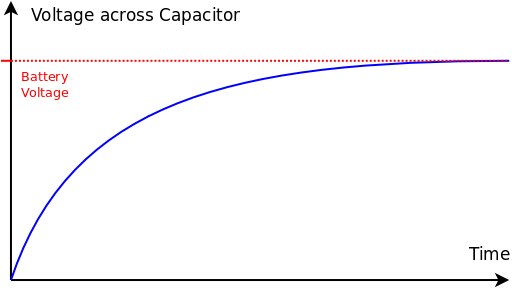 The gradient of the line at t = 0 is determined by the resistor
The gradient of the line at t = 0 is determined by the resistor
The maximum voltage across the capacitor is the battery voltage
Technically the curve is an exponential function
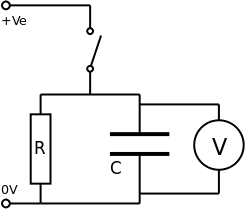
 The capacitor is initially fully charged; the voltmeter reads maximum voltage
The capacitor is initially fully charged; the voltmeter reads maximum voltage
When the switch is closed, current flows through the resistor and the capacitor discharges.
Initially the voltage across the resistor is high and the current is large so the capacitor discharges quickly.
After some time there is less charge on the capacitor (because it is discharging) and the voltage across the capacitor is smaller so the voltage across the resistor (in parallel) is also smaller and the current is reduced - the capacitor discharges more slowly
After a long time there is very little charge on the capacitor and therefore very little voltage across the capacitor and the resistor, the current is very low (almost zero) and the capacitor is (almost) fully discharged.
 The gradient of the line at t = 0 is determined by the resistor value.
The gradient of the line at t = 0 is determined by the resistor value.
The voltage across the capacitor reduces to (almost) zero as it discharges because the voltage across the capacitor depends on the charge on the capacitor
Technically the curve is an exponential decay function.
 Charging circuit
Charging circuit
The voltage across the capacitor and the voltage across the resistor add up to the battery voltage. As the capacitor charges up the voltage across the capacitor increases and so the voltage across the resistor must decrease.
As V = IR for the resistor, which means the resistor voltage and the current in the (series) circuit are proportional, the graph of current against time has the same shape as the green line (voltage across the resistor) albeit with a different scale.
 Discharging circuit
Discharging circuit
The voltage across the capacitor and the voltage across the resistor are the same because they are in parallel. As the capacitor discharges the voltage across the capacitor decreases and so the voltage across the resistor also decreases.
As V = IR for the resistor, which means the resistor voltage and the current in the circuit are proportional, the graph of current against time has the same shape as the blue line (voltage across the resistor and/or capacitor) albeit with a different scale.
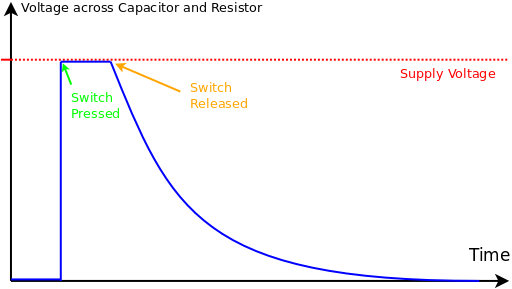
 The capacitor is initially uncharged and the reading on the voltmeter is zero
The capacitor is initially uncharged and the reading on the voltmeter is zero
The switch is pressed and the capacitor charges (almost) instantly because the resistance of the switch is very small and the current is high. The voltmeter shows the supply voltage because the capacitor is fully charged by the supply.
While the switch remains pressed the capacitor remains charged and the voltage on the voltmeter remains at the supply voltage.
When the switch is released the capacitor discharges through the parallel resistor and the voltage on the voltmeter reduces (exponentially) to zero.
 The circuit now includes two NOT gates. These act as buffers which means they take almost no current from the resistor - capacitor (RC) network. If the logic gates took any significant current they would affect the discharge time by making the capacitor discharge more quickly
The circuit now includes two NOT gates. These act as buffers which means they take almost no current from the resistor - capacitor (RC) network. If the logic gates took any significant current they would affect the discharge time by making the capacitor discharge more quickly
When the switch is pressed the voltage at A is HIGH, therefore the voltage at B is LOW (NOT gate) and the voltage at Q is HIGH. The LED is ON
When the switch is released the voltage across the capacitor does not immediately fall to zero, the voltage at A remains HIGH, the voltage at B remains LOW and the LED stays ON
After some time the voltage across the capacitor has reduced enough to become LOW and therefore the voltage at B is HIGH, this makes the voltage at Q go LOW and the LED is OFF
The LED stays ON for a fixed amount of time after the switch is released ... a simple timing circuit
 If Resistance (R) is in Ohms (Ω) and Capacitance (C) is in Farads (F) then the product (R × C) has units of time in seconds
If Resistance (R) is in Ohms (Ω) and Capacitance (C) is in Farads (F) then the product (R × C) has units of time in seconds
The product R × C is called the Time Constant and is a measurement of time in seconds - the time take for the RC Network to discharge to 36% of the initial voltage
In one time constant an RC network circuit will discharge to 36% of the initial voltage - this is a fact that can be shown mathematically
The graph shows the discharge of a capacitor over several time constants. The voltage starts at 10 volts and after one time constant the voltage has reduced to 3.6 volts.
The time constant is represented by the Greek letter Tao (τ) where τ = R × C
A capacitor is considered to be fully discharged after 5 time constants. After 5 time constants the charge (or voltage) on the capacitor is 36% of 36% of 36% of 36% of 36% of the initial charge which is about 0.6% of the initial charge. A capacitor is considered discharged when the remaining charge is less than 1% of the initial charge. Mathematically, 0.365 = 0.006.
 Knowing how long it takes an RC network to discharge to 36% of the initial value is not as useful as knowing how long it takes to discharge by half, i.e. to discharge to 50% of the initial value.
Knowing how long it takes an RC network to discharge to 36% of the initial value is not as useful as knowing how long it takes to discharge by half, i.e. to discharge to 50% of the initial value.
The time (T½) for an RC network to discharge to 50% is given by the equation
As shown on the graph, it takes one half value time (T½) to discharge from 8 volts to 4 volts. After another half value time (2T½ in total) the network has discharged from 4 volts to 2 volts. After 3 half value times (3T½) the voltage has reduced by half again to 1 volt
Example 1: An RC network is formed from a 12 kΩ resistor and a 220 µF capacitor. What is the time constant of the network? If the capacitor is initially charged to 16 volts, how long does it take to discharge to only 1 volt?
τ = 12 × 103 × 220 × 10−6 = 2.64 seconds
To discharge by 50% takes 0.7 × 2.64 = 1.85 seconds
To discharge from 16V to 1V is 4 half value times (16V → 8V → 4V → 2V → 1V) which is 4 × 1.85 = 7.4 seconds
Example 2: An RC network contains a 470µF capacitor and needs to discharge to half voltage in 10 seconds. What value of resistor should be used?
T½ = 0.7 × R × C and therefore R = T½ ÷ (0.7 × C)
R = 10 ÷ (0.7 × 470 × 10−6) = 30,400 Ω = 33 kΩ or 30 kΩ using the closest E24 series values
© Paul Nicholls
May 2020

Electronics Resources by Paul Nicholls is licensed under a Creative Commons Attribution 4.0 International License.